Raising the Compression Ratio.
How to do so safely and effectively, by measurement and calculation.
People often quote the Compression Ratio (CR) of an engine and a higher CR is considered an essential part of 'making it go faster'. But what is the CR, why is it important and how can it be raised safely, without risking damage to the engine?
Theory.
An internal combustion engine burns fuel to produce heat and energy. Although the conventional four strokes are often labelled "Induction, Compression, EXPLOSION, Exhaust", it is not true that the third stroke includes an explosion. The third stroke is really one of 'Combustion', or burning.
A pool of petrol (gasoline) will burn. Pour some into a plastic container and throw it in that fire. It will heat up, vaporize, and raise the pressure in the container until the plastic burns through. The confined petrol will burn very quickly, forming a fireball. (Don't try this at home, kids!) If you use a strong metal container, the petrol vapour will heat and compress, but the container will not melt. Eventually, if it gets hot enough and there is enough air in the container, the petrol vapour will get so hot and compressed that it will detonate. The spontaneous explosion may shatter the container, throw shrapnel about and make a loud noise. More heat, more compression and the fuel/oxygen reaction will happen more quickly and more efficiently.
As shown in this graph, a petrol engine will run more efficiently if the fuel/air mixture can be compressed as much as possible. BUT, too much compression and it will detonate, diesel style. The shock wave can easily shatter a four stroke piston.
A diesel engine is designed to compress its' fuel until the pressure and the increased heat produced by that compression cause the fuel to detonate. As a result, diesels have the advantage of high efficiency in terms of fuel use, but the disadvantage of needing to be very strongly constructed.
If the hotter, more compressed mixture is more efficient, why are all production engines not high compression for more power? There are several answers, including emissions as the extra heat produces more oxides of nitrogen (NOx), and less reliability as the engine is under greater strain. Fuel additives, including lead, and high octane petrol are necessary to allow reliable high compression without detonation. Fuel free of lead and benzene is all we have now, so modern engines have sensors and computer chips that adjust the ignition timing, so that they can run near the detonation point without being damaged.
But we want that power! If we are willing to put up with the downside, and without electronic engine management, how can we safely make the engine compress and heat the fuel more? By knowing the Compression Ratio.
The CR is a number, that shows how much the fuel/air mixture in the cylinder is compressed before it is ignited. The simplest way to calculate it is to take the stroke of the cylinder, the maximum volume of fuel/air, and divide it by the volume of the combustion chamber into which all that volume is compressed.
CR = Stroke volume
Combustion chamber volume
But that's too simple. When the piston is at the bottom of the stoke, the total volume in the cylinder includes the combustion chamber, so we must include that in the equation:
CR = (Stroke volume + Combustion chamber volume)/Combustion chamber volume
Again this is too simple. The head and block are separated by gasket, which has a definite thickness, so that the hole in the gasket for the bore has a volume - Gasket Volume.
An even smaller, but significant factor is the space in the bore, above the piston and below the top of the block, when the piston is at the top of its' stroke - "In Block" Volume. This can be made zero, or even negative if the pistons protrude out of the block at the top of the stroke, but only for very specialised purposes (See "Decking the block").
Thus the volume into which the stroke volume is compressed, the Compressed volume, is made up as follows:
Compressed Volume = Combustion Chamber Vol.+ Gasket Vol. + In Block Vol.
Thus, an accurate measurement of CR is made by:
CR = (Stroke volume + Compressed volume)/Compressed volume
(This is the Compression Ratio Equation)
In fact, this calculation is entirely theoretical! The actual compression ratio will be less, depending on how easily the fuel/air mix can get in and out of the cylinder. Flow through the carburettor and inlet ports, the shape and lift of the valves, the relation between inlet and exhaust lift of the camshaft and the design of the exhaust system are all factors. The less the resistance to flow and the better the exhaust gases leave and the new mixture enters, the nearer will practice be to theory.
Domes and Dishes.
A pitfall is the use of domed, or dished pistons. Some late 6 cylinder Triumphs had domed pistons, to reduce emissions, but none had dished pistons. A dome takes up space in, and should be deducted from, the Compressed Volume. A dish adds to the same volume and needs to be added. The volume of a dome can be estimated by calculation, or measured by a displacement method, but anyone wanting a performance engine should fit flat tops. See below and Appendix.
In Practice.
The CR of a standard Triumph varied with different models and markets. Early UK Spitfires were 9 to 1, while later versions for the USA emissions affected market were as low as 7 to 1. How high you raise your CR depends on how you feel about the downside, emissions and reliability, and on the fuel you have available.
The 'Octane number' of petrol tells how much compression it will stand without detonating. 100 octane petrol, meaning that it is as resistant to detonation as 100% octane, will be safe up to a CR of 11-12.5 to 1, but such high octane petrol is rarely available these days. You can run your engine on methanol with a CR of 14 or 15, but that is a different story! Better aim for no more than 10.5 to 1, which will be safe at 97 octane, but if you only have 95 octane, a CR of 9 should be your limit.
Calculating the CR
Our object is to raise the CR to a known, safe figure, and the method is to measure all the items listed in the equation:
CR = (Stroke volume + Compressed volume)/Compressed volume
Remembering that:
Compressed Volume = Combustion Chamber Volume + Gasket Volume + In Block Volume
Stroke volume we know, as long as you are sure of the engine type and can divide the total engine capacity by the number of cylinders. But blocks can be bored out. If you want to be totally obsessive, measure the cylinder bore and crank stroke, and use the equation:
V = π R2H
the volume of a cylinder with radius R and height H. (π = 'pi' = 3.1416)
Gasket volume can be measured in the same way, preferably from a good but used cylinder head gasket of the same type as you intend to use. Measure the hole for the cylinder, and the thickness of the gasket, and apply V = πR2H again. Don't use a new gasket for measurement, as it will be a lot thinner after it is fitted.
In Block Volume. Rotate the engine with the head off, and you will see that the pistons rise to nearly the top of the bore. Find top dead centre for each piston, and measure how far the piston is from the top of the block. Apply V = πR2H.
Ideally, the piston to block top distance should be identical for all the cylinders, but they may not be due to manufacturing tolerances. If one is very different, suspect an odd piston or even a worn big end, and deal with it.
"Decking the block" is a process in which a machine shop skims the higher pistons until they all rise to the same height, and then skims the block so that they come up as far as desired, usually to level with the block top. Then, the compressed volume is the same for all cylinders and all the cylinder CRs will be the same. This is expensive, time consuming and really not necessary unless you are going for a full race engine.
Combustion Chamber Volume(CCV). There is only one way to measure the CCV, and that is by pouring a known volume of a liquid into the chamber until it is full! To do this accurately you need a chemist's burette, that you may remember seeing and using in school chemistry. Your local school may be able to help you find out where to buy one, because they aren't for sale in the local hardware shop. Buy, or make, a burette stand, to mount the burette vertically on the bench.
You also need a sheet of glass a bit bigger than the cylinder bore. Below is a diagram of the square I use. Your local glaziers will have lots of pieces this big in their scrap bin, but ask for plate glass, ¼"(6mm) thick so that it is durable. Get them to chamfer the edges and corners to protect your fingers.
Put the cylinder head on your bench, chambers up. Arrange some chocks to make it level, secure and high enough to allow the valves to seat. Put the valves in place, with a little grease to seal them. Don't forget the spark plug! Place your glass square over the chamber, again with a little grease around it to seal it to the face of the head. Both holes should be over the chamber.
Position your burette so that it will drip into the chamber via one of the holes, and fill the burette. Water is useless, as it will not 'wet' the metal and leaves bubbles to confuse your measurements. Some people use paraffin (USA = kerosene?) but it gets everywhere, and I hate the smell, so I use 'Liquid paraffin'. You should be able to find this in 100 ml bottles at your local pharmacist (druggist?), who may think that you wish to use it to treat your constipation! Liquid paraffin is a light mineral oil, that wets metal surfaces but is water soluble, so it is easy to clean up and doesn't smell!
Note the volume of liquid in the burette, and open the tap to run it into the chamber. Go slowly, to avoid bubbles and splashing. When the chamber is nearly full, add the liquid drop by drop. You may have to tilt the head around a little to persuade the last bubbles to leave. The very last bit of filling is into the thickness of the glass cover, so you may need to practise a bit, and to find an endpoint at which you decide that it is full. Use the same endpoint for each cylinder, or you will not be able to tell if they are same size. Read the remaining volume in the burette and work out the volume you have run in. That is the Combustion Chamber volume!
Measure each chamber. It is even more important than the actual volume that all the chambers should be the same, within +/- 0.5mls. There are about 15 drops to the millilitre, so you should be able to measure the volume to less than +/- 0.1mls.
Alternatives to the burette.
If you have access to disposable medical syringes, these are an excellent alternative. Try and get a 20mls size, for the major filling, and a 2ml size for final topping up, so that you can measure down to 0.1mls.
How to use the measurements.
Now you can work out your present Compression Ratio, that you want to change.
Compressed volume
(Remember that Compressed Volume = Combustion Chamber Volume + Gasket Volume + In Block Volume)
While it may interesting to know exactly the present CR, you may think that we knew that already, from the model, year and possibly engine number of the car. Sadly, not so! The previous owner may have modified the engine, or have fitted an engine from a different model. If you assume that the CR is the same as when it left the factory and that it will be safe to skim 'X' thousandth of an inch off the head, you will risk ruining the cylinder head. Now that you know the true CR, you can work out how much to skim to raise the CR precisely to the level that you want.
Calculating the skim to achieve a raised CR.
First, work the CR equation backwards from the CR that you want, to the smaller CCV required to get it. All the other quantities will stay the same.
First you must calculate the new compressed volume that includes the CCV:
Sparing you the algebra:
The Gasket Volume and In Block volume will not change if you skim the head, unless you deck the block as well, so subtract them from the NEW Compressed volume:
New Combustion Chamber Volume =
Then:
Volume to be removed by skimming = Measured Combustion Chamber Vol. - New Combustion Chamber Vol.
Now work V= πR2H backwards, from volume V to height H. Again, sparing you the algebra:
H= V/ πR2
Or
Pi x radius squared
This is the height or thickness that must be skimmed from the head!
Yes, I know that this equation assumes that the combustion chamber is circular, when clearly it is not! However, the difference from a circle is small enough not to matter. For R use the average of the widest and narrowest width of the chamber, but remember to divide the width by 2, to get a radius.
If you want to be as accurate as possible, measure the area of the chamber directly. Place a piece of graph paper over a chamber, and rub your dirty thumb, or a soft pencil across the edges. From this outline of the chamber, count the squares of the graph paper, and multiply the number of squares by the area of each square.
Use this in the above equation, replacing the πR2 with 'Area', and calculate
H = V/Area
Units.
You can use Imperial or Metric, but burettes are always calibrated in millilitres. Be very certain that you use the same units all the way through, to get an answer in centimetres or decimal inches. NASA crashed a Mars probe by making just this mistake!
The Domed Piston.
Late six cylinder Triumphs, and I think some US Spitfires, were fitted with domed pistons, in an attempt to meet emissions regulations. The dome slows combustion, just what we are trying to speed up, so if possible get yourself a set of flat tops. If you must keep the domes, do not forget that these stick up into the combustion chamber. Their volume must be subtracted from the CCV before doing the CR calculation.
The problem is, what is the volume of the dome? Triumph six cylinder domes are 8.66mls, but I regret that I have never seen a Spitfire dome, so I cannot say what its volume would be. The Appendix explains how the dome volume can be calculated from direct measurements of a domed piston. Note the effect on CR that the dome can make!
If you don't trust such esoteric calculations, measure the dome directly. Fit a domed piston in the bore, complete with greased piston rings and so deep that the dome is just below the top of the block. The actual depth does not matter. Measure the depth of the piston at the bore wall. Calculate the apparent volume of this cylinder using V= πR2H.
Now use the burette method, as used to measure the Combustion chamber volume, to measure the real volume of the bore above the piston. This will be less than the apparent volume you measure above, and the difference is the volume of the dome.
ERRATUM! (01/10/05) Domed pistons. The first sentences of the above section is completely wrong! NO Spitfires were fitted with domed pistons, only cars with 2000 engines. The reason was nothing to do with emissions, but with commonality.
Triumph used the same cylinder head casting, with the same combustion chamber shape for both the 2000 and the 2500 engine. Because the 2000 needed a smaller combustion chamber, more would be machined off the face of the head to make the chamber less high.
Then someone realised that if they used a dome that took up the same volume as the difference in chamber volume between the 2000 and 2500, they could use the same head for both engines. I presume that a domed piston took only a little or no more machining than a flat one, but I don't know enough about production engineering. Whatever, it must have taken less time, less work and cost less - brilliant management! So unusual for Triumph!
This change took place from T2000 engine No. ME 50000 and GT6 engine No. KC 10001.
I am indebted to Andy Thompson of Perth, Western Australia and John Thomason's excellent Originality Guide for this information, which I should have known before writing this article!
However, a dome does slow combustion, and I stand by my previous comments about it for a performance engine and on measuring a dome.
High lift camshafts.
Further performance modifications can include re-grinding the camshaft, and/or roller rockers, with a higher leverage ratio. High duration, high lift cams bring the valves further into the combustion chamber, for longer during the cycle. Roller rockers will increase this still more. Reduce the chamber height for a maximum CR, and the valves could collide with the piston. If you persist in using domed pistons with all that, then they will collide!
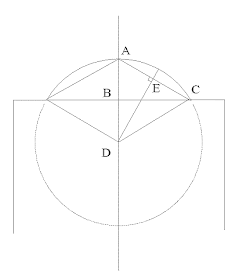
Appendix. Measuring the volume of a dome.
A circular dome is a sector of a sphere. Imagine a horizontal slice from the top of an orange. At the centre of the sphere, the circumference of the sector forms an angle with the 'North-South' axis of the sphere. If the sector is half the orange, the angle will be 90 degrees. If the sector is smaller, so will the angle.
Where R is the radius of the sphere, the volume of a sector of a sphere is:
Volume= π x R3 x [2 - 3xCos(angle) + Cos (angle) 3]
3
The size of the angle is measured in degrees. If the radius of the sphere is in centimetres, the volume will be in cubic centimetres, or millilitres.
That's fine, but how to measure the radius of this imaginary sphere of which our dome is a sector? You can, by measuring the dome, and applying some more trigonometry.
The diagram shows a side view of the sphere and sector. D is the sphere's centre, BC the plane that divides the sector from the rest of the sphere. AD and CD are radii, the first forming a right angle with the plane, BC. By measurement, we know the diameter of the sector or dome, which is twice BC, and the height of the dome, AB. We need to calculate the angle at the centre, which is twice the angle ADC, and the radius of the sphere, AD.
First, consider the right angled triangle ABC. Calculate AC, by Pythagoras.
AC = Ö (AB2+ BC2)




No comments:
Post a Comment